Optimistic Gradient Descent in a Bilinear Min-Max Problem

import jax
import jax.numpy as jnp
import optax
import matplotlib.pyplot as plt

Consider the following min-max problem:

\[ \min_{x \in \mathbb R^m} \max_{y\in\mathbb R^n} f(x,y), \]

where \(f: \mathbb R^m \times \mathbb R^n \to \mathbb R\) is a convex-concave function. The solution to such a problem is a saddle-point \((x^\star, y^\star)\in \mathbb R^m \times \mathbb R^n\) such that

\[ f(x^\star, y) \leq f(x^\star, y^\star) \leq f(x, y^\star). \]

Standard gradient descent-ascent (GDA) updates \(x\) and \(y\) according to the following update rule at step \(k\):

\[ x_{k+1} = x_k - \eta_k \nabla_x f(x_k, y_k) \\ y_{k+1} = y_k + \eta_k \nabla_y f(x_k, y_k), \]

where \(\eta_k\) is a step size. However, it’s well-documented that GDA can fail to converge in this setting. This is an important issue because gradient-based min-max optimisation is increasingly prevalent in machine learning (e.g., GANs, constrained RL). Optimistic GDA (OGDA) addresses this shortcoming by introducing a form of memory-based negative momentum:

\[ x_{k+1} = x_k - 2 \eta_k \nabla_x f(x_k, y_k) + \eta_k \nabla_x f(x_{k-1}, y_{k-1}) \\ y_{k+1} = y_k + 2 \eta_k \nabla_y f(x_k, y_k) - \eta_k \nabla_y f(x_{k-1}, y_{k-1})). \]

Thus, to implement OGD (or OGA), the optimiser needs to keep track of the gradient from the previous step. OGDA has been formally shown to converge to the optimum \((x_k, y_k) \to (x^\star, y^\star)\) in this setting. The generalised form of the OGDA update rule is given by

\[ x_{k+1} = x_k - (\alpha + \beta) \eta_k \nabla_x f(x_k, y_k) + \beta \eta_k \nabla_x f(x_{k-1}, y_{k-1}) \\ y_{k+1} = y_k + (\alpha + \beta) \eta_k \nabla_y f(x_k, y_k) - \beta \eta_k \nabla_y f(x_{k-1}, y_{k-1})), \]

which recovers standard OGDA when \(\alpha=\beta=1\). See Mokhtari et al., 2019 for more details.

\[ \pi^{k+1} = \pi^k - \tau_\pi^k \nabla_\pi \mathcal L(\pi^k, \mu^k) \\ \mu^{k+1} = \mu^k + \tau_\mu^k \nabla_\mu \mathcal L(\pi^k_k, \mu^k), \]

\[ \pi^{k+1} = \pi^k - 2\tau_\pi^k \nabla_\pi \mathcal L(\pi^k, \mu^k) + \tau_\pi^k \nabla_\pi \mathcal L(\pi^{k-1}, \mu^{k-1})\\ \mu^{k+1} = \mu^k + 2\tau_\mu^k \nabla_\mu \mathcal L(\pi^k_k, \mu^k)+ \tau_\mu^k \nabla_\mu \mathcal L(\pi^{k-1}, \mu^{k-1}) \]

where \(\eta_k\) is a step size. However, it’s well-documented that GDA can fail to converge in this setting. This is an important issue because gradient-based min-max optimisation is increasingly prevalent in machine learning (e.g., GANs, constrained RL). Optimistic GDA (OGDA) addresses this shortcoming by introducing a form of memory-based negative momentum:

\[ x_{k+1} = x_k - 2 \eta_k \nabla_x f(x_k, y_k) + \eta_k \nabla_x f(x_{k-1}, y_{k-1}) \\ y_{k+1} = y_k + 2 \eta_k \nabla_y f(x_k, y_k) - \eta_k \nabla_y f(x_{k-1}, y_{k-1})). \]

Define a bilinear min-max objective function: \(\min_x \max_y xy\).

def f(params: jnp.ndarray) -> jnp.ndarray:
  """Objective: min_x max_y xy."""
  return params["x"] * params["y"]

Define an optimisation loop.

def optimise(params: optax.Params, x_optimiser: optax.GradientTransformation, y_optimiser: optax.GradientTransformation, n_steps: int = 1000, display_every: int = 100) -> optax.Params:
  """An optimisation loop minimising x and maximising y."""

  x_opt_state = x_optimiser.init(params["x"])
  y_opt_state = y_optimiser.init(params["y"])
  param_hist = [params]
  f_hist = []

  @jax.jit
  def step(params, x_opt_state, y_opt_state):
    f_value, grads = jax.value_and_grad(f)(params)
    x_update, x_opt_state = x_optimiser.update(grads["x"], x_opt_state, params["x"])
    # note that we"re maximising y so we feed in the negative gradient to the OGD update
    y_update, y_opt_state = y_optimiser.update(-grads["y"], y_opt_state, params["y"])
    updates = {"x": x_update, "y": y_update}
    params = optax.apply_updates(params, updates)
    return params, x_opt_state, y_opt_state, f_value

  for k in range(n_steps):
    params, x_opt_state, y_opt_state, f_value = step(params, x_opt_state, y_opt_state)
    param_hist.append(params)
    f_hist.append(f_value)
    if k % display_every == 0:
      print(f"step {k}, f(x, y) = {f_value}, (x, y) = ({params['x']}, {params['y']})")

  return param_hist, f_hist

Initialise \(x\) and \(y\), as well as optimisers for each.

initial_params = {
    "x": jnp.array(1.0),
    "y": jnp.array(1.0)
}

# GDA
x_gd_optimiser = optax.sgd(learning_rate=0.1)
y_ga_optimiser = optax.sgd(learning_rate=0.1)

# OGDA
x_ogd_optimiser = optax.optimistic_gradient_descent(learning_rate=0.1)
y_oga_optimiser = optax.optimistic_gradient_descent(learning_rate=0.1)

Run each method.

gda_hist, gda_f_hist = optimise(initial_params, x_gd_optimiser, y_ga_optimiser)

step 0, f(x, y) = 1.0, (x, y) = (0.8999999761581421, 1.100000023841858)
step 100, f(x, y) = 1.2648853063583374, (x, y) = (-0.3346042335033417, -2.3133885860443115)
step 200, f(x, y) = -4.116152286529541, (x, y) = (-1.4915204048156738, 3.5431253910064697)
step 300, f(x, y) = -19.666868209838867, (x, y) = (5.107692718505859, -3.726156711578369)
step 400, f(x, y) = -19.6387939453125, (x, y) = (-10.357627868652344, 0.9156706929206848)
step 500, f(x, y) = 94.20153045654297, (x, y) = (15.369263648986816, 7.498481750488281)
step 600, f(x, y) = 381.9855651855469, (x, y) = (-15.290411949157715, -23.605133056640625)
step 700, f(x, y) = 277.15576171875, (x, y) = (1.5127239227294922, 46.23002243041992)
step 800, f(x, y) = -2093.469482421875, (x, y) = (37.095298767089844, -66.4145736694336)
step 900, f(x, y) = -7323.67138671875, (x, y) = (-108.61480712890625, 62.09233474731445)

ogda_hist, ogda_f_hist = optimise(initial_params, x_ogd_optimiser, y_oga_optimiser)

step 0, f(x, y) = 1.0, (x, y) = (0.800000011920929, 1.2000000476837158)
step 100, f(x, y) = 0.031045246869325638, (x, y) = (0.050776559859514236, -0.8584850430488586)
step 200, f(x, y) = -0.12628404796123505, (x, y) = (-0.33432960510253906, 0.3951655626296997)
step 300, f(x, y) = -0.029761798679828644, (x, y) = (0.3036675751209259, -0.06965611129999161)
step 400, f(x, y) = 0.010520423762500286, (x, y) = (-0.17140555381774902, -0.07605954259634018)
step 500, f(x, y) = 0.006046054419130087, (x, y) = (0.05510440468788147, 0.09850382059812546)
step 600, f(x, y) = -0.00015094212722033262, (x, y) = (0.009013960137963295, -0.06733492761850357)
step 700, f(x, y) = -0.0008242211770266294, (x, y) = (-0.028646370396018028, 0.029178569093346596)
step 800, f(x, y) = -0.0001478429330745712, (x, y) = (0.02432975359261036, -0.003714002436026931)
step 900, f(x, y) = 7.810298848198727e-05, (x, y) = (-0.013059122487902641, -0.006993034854531288)

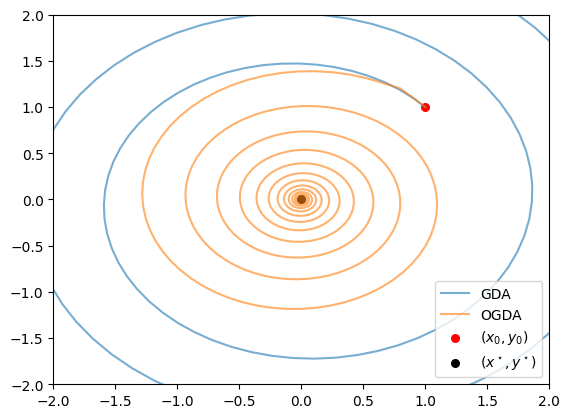
Visualise the optimisation trajectories. The optimal solution is \((0, 0)\).

gda_xs, gda_ys = [p["x"] for p in gda_hist], [p["y"] for p in gda_hist]
ogda_xs, ogda_ys = [p["x"] for p in ogda_hist], [p["y"] for p in ogda_hist]

plt.plot(gda_xs, gda_ys, alpha=0.6, color="C0", label="GDA")
plt.plot(ogda_xs, ogda_ys, alpha=0.6, color="C1", label="OGDA")
plt.scatter([1], [1], color="r", label=r"$(x_0, y_0)$", s=30)
plt.scatter([0], [0], color="k", label=r"$(x^\star, y^\star)$", s=30)
plt.xlim([-2.0, 2.0])
plt.ylim([-2.0, 2.0])
plt.legend(loc="lower right")
plt.show()